How To simplify rational expressions step-by-step Using algebra 2 help
Wiki Article
The Comprehensive Protection of Algebra 2 Tutoring: Trick Concepts and Skills for Proficiency
Algebra 2 tutoring offers a broad spectrum of important concepts and skills needed for pupils to achieve mastery in mathematics. This incorporates an extensive understanding of polynomial functions, complicated numbers, and logarithmic formulas, amongst others. Each subject develops on the previous one, developing a natural framework for problem-solving. The application of these concepts in real-world situations highlights their significance. Yet, there remain important locations that can better boost a student's mathematical trip.Recognizing Polynomial Features
Just how do polynomial features form the landscape of algebra? These essential expressions, containing variables increased to non-negative integer powers, offer as the foundation of lots of algebraic ideas. They can be defined by their degree, which indicates the greatest power of the variable, and their coefficients, which figure out the function's behavior. Polynomial functions show distinctive residential properties, such as continuity and smoothness, enabling them to design a variety of real-world scenarios. Their visual representations feature contours that can demonstrate various behaviors, including intercepts and turning points. Understanding polynomial functions includes understanding operations such as addition, department, reduction, and reproduction, as well as factoring strategies. This fundamental knowledge is essential for solving formulas and inequalities. By comprehending polynomial features, pupils establish important analytic abilities and gain understanding right into extra complex mathematical concepts, paving the method for advanced research studies in algebra and past.Mastering Intricate Numbers
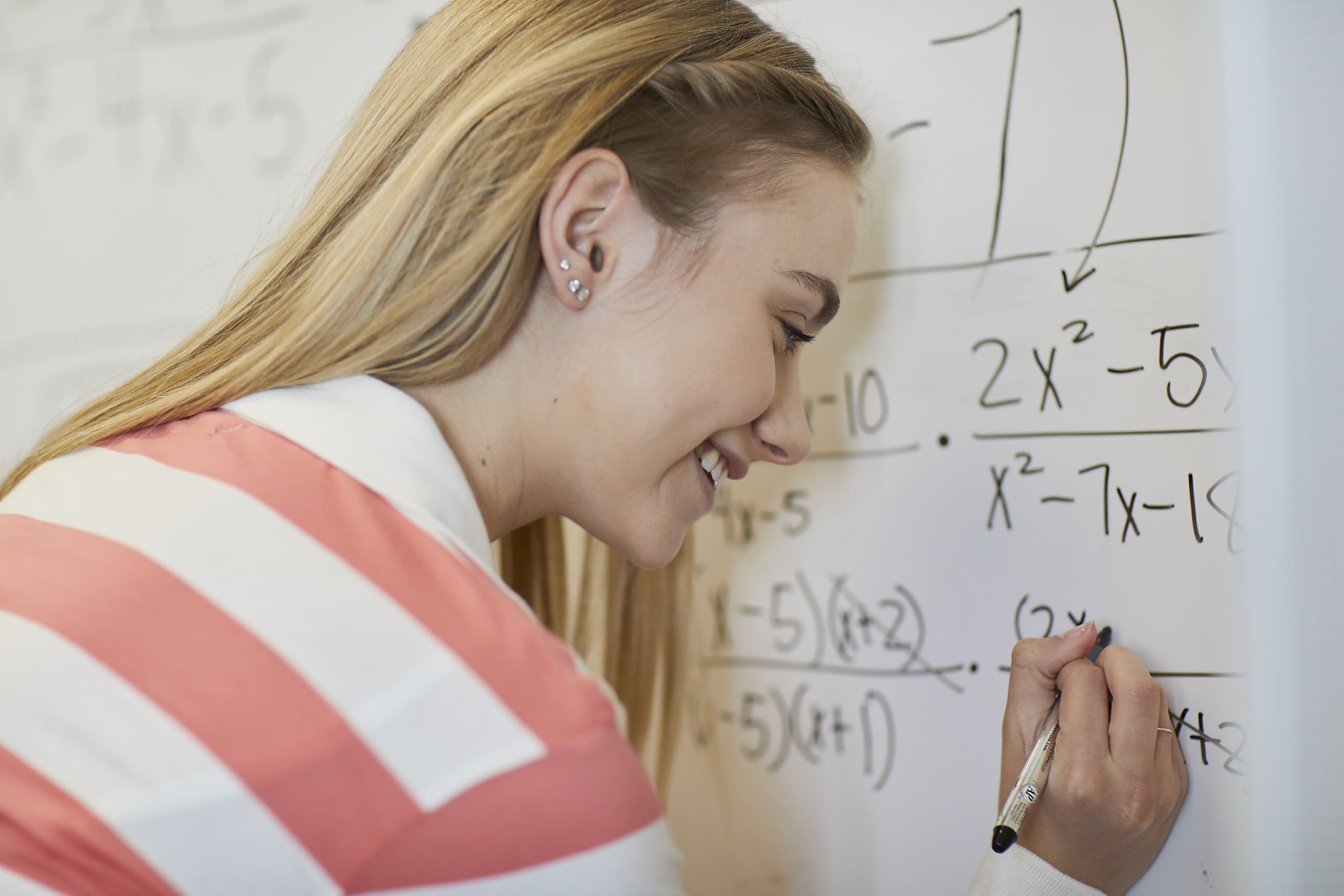
Meaning and Properties
Complex numbers, a keystone of sophisticated algebra, prolong the concept of one-dimensional number lines to a two-dimensional plane. Specified as varieties of the kind (a + bi ), where (a) and (b) are real numbers and (i) represents the fictional unit with the residential property (i ^ 2 = -1 ), these numbers have distinct homes. The genuine part (a) suggests the straight axis, while the fictional part (b) suggests the vertical axis in the complex plane. Trick buildings include their ability to represent solutions to polynomial equations that lack genuine solutions and their closure under enhancement, reproduction, division, and subtraction (except by absolutely no) This framework permits a much deeper understanding of mathematical ideas and applications throughout numerous areas.Procedures With Complicated Numbers
Operations with complex numbers develop a crucial aspect of algebra that improves mathematical understanding and problem-solving capacities. Complex numbers, revealed in the kind (a + bi), where (a) and (b) are actual numbers, need particular operations like enhancement, multiplication, reduction, and department.Addition and reduction entail combining like terms, while multiplication uses the distributive residential property and the reality that (i ^ 2 = -1) Department of intricate numbers necessitates multiplying the numerator and by the conjugate to remove the fictional component in the denominator. online algebra 2.
These procedures not only reinforce fundamental algebra skills yet additionally prepare trainees for even more innovative topics, such as polynomial formulas and square features. Proficiency of complex number procedures equips students with important logical devices.
Checking Out Logarithmic Formulas
In the research of logarithmic equations, recognizing the homes of logarithms is crucial for reliable analytical. These homes supply the foundational tools required to adjust and streamline logarithmic expressions. By mastering these principles, trainees can with confidence take on a variety of logarithmic formulas.Recognizing Logarithm Qualities
Logarithm residential properties play an essential function in simplifying and addressing logarithmic equations, providing a methodical strategy to comprehending their habits. These buildings include the power, ratio, and item rules. The product guideline mentions that the logarithm of a product is the sum of the logarithms of its factors. Conversely, the quotient policy indicates that the logarithm of a quotient is the distinction of the logarithms. The power rule discloses that the logarithm of a number increased to a backer can be shared as the backer multiplied by the logarithm of the base. Proficiency of these properties enhances one's ability to adjust logarithmic expressions, algebra 2 help offering a foundation for tackling much more complex equations and functions encountered in innovative algebra.Addressing Logarithmic Equations
Exactly how can one properly fix logarithmic equations? To take on these formulas, it is crucial to use residential properties of logarithms. One ought to combine logarithmic expressions making use of the power, quotient, and product policies. This simplification usually transforms the formula into a much more workable kind. Next off, transforming logarithmic equations to their rapid kind can disclose the unidentified variable. As an example, the formula (log_b(x) = y) translates to (x = b ^ y ) Additionally, checking services is important to assure they do not create additional outcomes, particularly when handling logarithms. By methodically applying these techniques, individuals can confidently browse and solve logarithmic equations, boosting their total understanding and proficiency of this mathematical principle.Examining Sequences and Series
Sequences and collection might at first show up facility, they are fundamental principles in algebra that disclose patterns and connections within numbers. A sequence is a listing of numbers organized in a particular order, typically specified by a formula or rule. Recognizing the kinds of series, such as math and geometric sequences, enables trainees to recognize the underlying patterns successfully.On the various other hand, a series is the sum of the regards to a series. Evaluating collection includes identifying unlimited and finite series, along with computing their amounts when applicable. Pupils learn crucial strategies, such as making use of formulas for the amount of math and geometric series, which improve computations.
Understanding series and series outfits pupils with important problem-solving skills, allowing them to deal with more complex mathematical principles. This foundation is essential for their proceeded success in algebra and higher-level mathematics.
Resolving Logical Expressions and Formulas

When fixing reasonable formulas, one must separate the variable, often by cross-multiplying to remove the fractions. It is essential to look for extraneous options, as multiplying both sides can present worths that do not satisfy the initial formula. Additionally, students must know limitations on the variable, as certain values can make the common denominator absolutely no, making the expression undefined.
Grasping Conic Sections
Conic areas are geometric figures acquired from the crossway of a plane and a dual cone. These areas include circles, ellipses, parabolas, and hyperbolas, each identified by unique residential or commercial properties and formulas. Comprehending conic areas is vital for students as they discover the connections between algebra and geometry.
Circles are specified by a consistent range from a center factor, while ellipses result from an airplane cutting through both cones, forming a shut contour. Parabolas develop from an aircraft alongside the axis of the cone, portraying a U-shaped chart. Hyperbolas, on the various other hand, take place when the aircraft halves both intersects of the cone, leading to 2 unique, open curves.
In Algebra 2, grasping conic areas involves acknowledging their common formulas, graphing them accurately, and identifying their vital attributes, such as vertices, emphases, and axes. This foundational expertise prepares pupils for even more innovative mathematical principles.
Using Charts and functions
Graphs and features serve as fundamental devices in Algebra 2, allowing students to design connections in between variables and picture mathematical principles. Proficiency of these aspects enables learners to analyze information, recognize trends, and make predictions based upon recognized patterns. Pupils discover different kinds of features, including linear, quadratic, polynomial, sensible, and exponential, each with distinct features and applications.Graphing these functions entails comprehending essential features such as inclines, intercepts, and asymptotes, which supply insights right into their habits. In addition, pupils find out to transform functions via representations, shifts, and stretches, improving their capacity to adjust and analyze visual representations.
Using functions in real-world contexts further strengthens understanding, as trainees tackle issues entailing profit margins, population development, and physics equations. This functional application bridges academic expertise with concrete results, cultivating a much deeper appreciation for the significance of features and graphs in daily life.
Frequently Asked Questions
Exactly How Can I Improve My Problem-Solving Abilities in Algebra 2?
To boost analytic abilities in Algebra 2, one need to exercise frequently, look for diverse issues, utilize on the internet resources, team up with peers, and concentrate on understanding underlying principles instead of remembering treatments, cultivating deeper understanding and application.What Resources Are Suggested for Extra Algebra 2 Practice?
Recommended sources for extra Algebra 2 practice include online platforms like Khan Academy, textbooks with method issues, and tutoring services. Taking part in mathematics discussion forums can likewise give varied analytical methods and joint discovering possibilities.Exist Online Tutoring Options Available for Algebra 2?
Yes, numerous online tutoring alternatives exist for Algebra 2 (online algebra 2). Platforms like Khan Academy, Chegg Tutors, and Wyzant deal personalized aid, video clip lessons, and interactive exercises, satisfying different discovering designs and timetables for pupils seeking assistanceExactly how Do I Prepare for Algebra 2 Examinations Efficiently?
To prepare properly for Algebra 2 tests, one ought to evaluate vital concepts, practice troubles consistently, make use of online sources, develop study hall, and take practice tests to determine staminas and fancies targeted improvement.
What Prevail Misconceptions Pupils Have in Algebra 2?
Students commonly misinterpret the significance of foundational concepts, thinking they can skip prerequisites. They may additionally deal with abstract thinking, perplexing features with formulas, and misinterpreting the duty of variables in algebraic expressions.Mastering intricate numbers is vital for trainees in Algebra 2, as these numbers prolong the genuine number system to solve formulas that lack actual services. These operations not only reinforce foundational algebra abilities yet also prepare students for even more innovative topics, such as square functions and polynomial equations. Sensible expressions and equations represent crucial elements of algebra, including fractions where the numerator and denominator are polynomials. In Algebra 2, grasping conic sections involves identifying their typical equations, graphing them properly, and identifying their crucial functions, such as axes, vertices, and foci. Applying features in real-world contexts additionally solidifies understanding, as trainees deal with troubles involving profit margins, population growth, and physics equations.
Report this wiki page